Матэсприматика.
Лектор:
Тема сегодняшней лекции: Начала Интегрального Исчисления.
Идите все, идите за Урал.
Мы расчищаем место бою
Стальных машин, где дышит интеграл
С монгольскою ордою.
А.Блок, «Скифы»
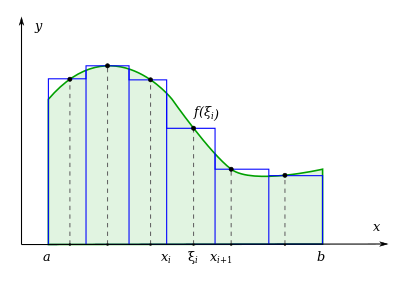
Итак, перед нами (См картинку) зачерченный график некой кривой.
Дана некая непрерывная функция и мы хотим взять её интеграл по «у» в промежутке от «а» до «b».
Кривая может быть любой формы, но для простоты сделаем допущение, что мы ЗНАЕМ функцию, ограничивающую зачерченную площадь сверху.
Скажем, что фигура эта – криволинейная трапеция
Наша задача – вычислить площадь этой фигуры.
Предлагайте свои решения!
Студент №1: Предлагаю «выпрямить» кривую и затем подсчитать площадь прямоугольника.
Студент №2: Моё предложение является как бы продолжением первой идеи: Усреднить площадь под только кривой и сложить с площадью оставшегося прямоугольника.
Студент №3: Предлагаю разбить всю площадь на вертикально стоящие прямоугольники и подсчитать их площадь, конечно, я понимаю, что это не будет очень точно, но лектор ведь умолчал о разрешённой ошибке в определении…
Лектор: Совершенно верное замечание. Добавлю, «с максимально возможной точностью, в пределе – математически точно!
Студент №4: Ну, это невозможно, даже если бы мы измеряли площадь каким-нибудь специальным прибором, для этого приспособленным. Каким-нибудь планиметром? Ведь любой прибор даёт ошибку!
Лектор: Но, всё же, как нам ПРИБЛИЗИТЬСЯ к идеалу?
Студент №5: Я думаю, мы должны увеличить число прямоугольничков, тогда будет точнее.
Студент №4: Так ведь опять измеренная площадь будет лишь приблизительно оценена!
Лектор: Я прошу обратить внимание на одно моё слово, которое я произнёс с ударением: ПРИБЛИЗИТЬСЯ!
Студент№5: Я думаю, надо уменьшать толщину приямоугольничков, тогда получающееся ступенчатое тело будет ПРИБЛИЖАТЬСЯ по своей площади к искомой .
Лектор: Идея разумная, но чем тоньше прямоугольнички, тем МЕНЬШУЮ площадь они будут захватывать! Получится некая кривая, «опирающаяся на тоненькие столбики» прямоугольничков.
Студент №4. А вот это уже лучше – будем увеличивать число прямоугольничков!
Стулдент №5: Я понял! Надо БЕСКОНЕЧНО уменьшать толщину каждого прямоугольничка и ОДНОВРЕМЕННО, бесконечно увеличивать их число. Ведь они должны заполнять всё пространство под кривой «крышей»! Получится сумма бесконечно тонких прямоугольничков взятых в бесконечно большом количестве.
Студет №3: Так, ведь тогда наша площадь получится бесконечной большой!
Студент№4: Нет, номер пятый прав! Ведь видно на графике, что площадь, заключённая между осью координат, двумя вертикальными прямыми и кривой, ОГРАНИЧЕНА! Куда ж ей расти, если со всех сторон границы?!
Лектор: Вот мы и придумали интегральное исчисление, именно:
Конечный предел бесконечно большой суммы бесконечно малых величин!
А видов интегралов много: Определённые, неопределённые, собственные, несобственные, криволинейные, эллиптические, двойные, тройные интегралы, интегралы Лебега, Зоммерфельда, Фурье, Френеля, Римана, Эйлера и ещё немало других, не говоря уже об интегральных уравнениях.
Но об этом во всех последующих лекциях.
Поздравляю всех с открытием!
Обычное признание: Не математик я и туп к математике, как некая часть носорога, полярно противоположная его голове…
12 XII 2017