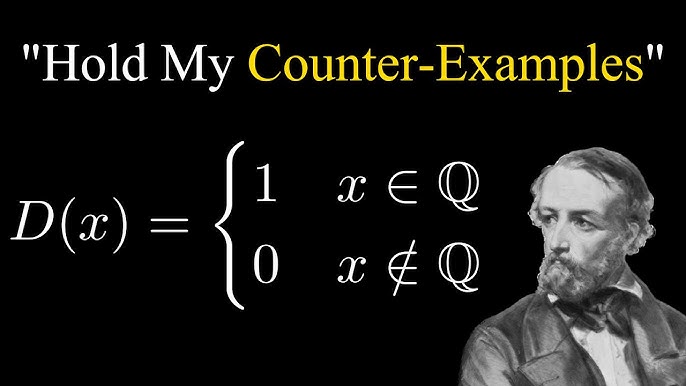
This is a question of professional analphabet (simply, ignoramus) in mathematics to professional mathematicians.

The most likely answer is:

That’s an idiotic question! WHAT does the author mean by asking about love or dislike for some mathematical concept or branch of mathematics?

Is it the same as asking if mathematicians like operators or prefer matrices to them? Or that they don’t like differentiation, but they like integration!

The utter cretinism of such a question is obvious!

Maybe they’re right.

But in my defense, I would like to note that Heisenberg developed the mathematical apparatus of Quantum mechanics precisely on the basis of matrix mechanics, while Schroedinger used operators for his “Wave Mechanics” (The same Quantum mechanics).

Let me also remind you that the famous English mathematician Littlewood said about another Indian mathematician, Ramanujan, that “all natural numbers were his personal friends”! (I read about it, I think, in his interesting book “Mathematical Mixture”,)

Mathematicians are also human beings, and “nothing human is alien to them.”

People can either feel attachment to certain concepts, words, expressions, style, or, equally, dislike it.

Rossini, for example, could not stand Wagner’s MUSIC.

So. my question doesn’t seem so idiotic. And, moreover, I will try to answer it:

THEY DON’T LIKE IT!

And, it seems to me, they are trying in some way to turn them into INSEPARABLE, CONTINUOUS ONES!

The age-old question is: Why?

It seems to me that because of purely human, and non–human, thinking, humans and animals do not like the unpredictability of something. This is a purely biological instinct of ALL living beings, because it carries with it an existential threat. Danger of death!

This means that mathematicians like to study a certain function in detail, and by creating an algorithm for its “behavior”, they mathematically approximate the past and future “behavior” of this CONTINUOUS projection!

But it is IMPOSSIBLE to do this with discontinuous ones, here we already have to talk about “random, stochastic, probabilistic processes.” It is impossible to accurately predict and approximate anything in them.

I once described the method of thinking mathematics using the example of a crawling caterpillar. But mathematics CANNOT predict that at some point the caterpillar will stop eating, and, having attached itself to a leaf, it will suddenly begin to rotate, wrapping itself in a kind of rapidly solidifying thread, which it releases and encloses itself in a kind of IMPENETRABLE solid cocoon!

This dislike of mathematics for discontinuous functions is due to one more thing: If there is a break in a certain function and a complete detachment from the previous move after it, then one inevitably has to ask the question: WHY?

Why is there a sudden gap?

Why would there suddenly be such a radical change in the course of a function that had been continuous and PREDICTABLY smoothly developing for a very long time before it broke?

And mathematics is not interested in such a question and never asks it. This question relates to a SPECIFIC TOPIC OF CAUSALITY, conditioning, and determinism. And mathematics is inherently indeteministic, its concreteness (and THE REASON IS ALWAYS SPECIFIC!!!) not interested!

Such things, as one of my friends used to say.

If I’m wrong, let my seniors correct me.

14 VIII 2025